FLUIDES (MÉCANIQUE DES)

FLUIDES (MÉCANIQUE DES)

La mécanique des fluides constitue l’extension de la mécanique rationnelle à une classe de milieux continus dont les déformations peuvent prendre des valeurs aussi grandes que l’on veut. On désigne sous le nom général de fluides des corps matériels, gaz, liquides et plasmas, qui peuvent se mettre sous une forme quelconque lorsqu’ils sont soumis à un système de forces, ces forces pouvant être aussi faibles que l’on veut, à condition qu’on les fasse agir pendant un temps assez long. Cette définition permet d’exclure les corps plastiques, qui se comportent comme des solides tant que les contraintes en leur sein ne dépassent pas un certain seuil.

Ainsi, comme en mécanique rationnelle, on distingue une cinématique, une statique et une dynamique des fluides. Le principe de conservation de l’énergie et la loi fondamentale de la dynamique, compte tenu des forces de contact qui dépendent des vitesses de déformation du fluide, s’appliquent à des éléments de volume du fluide infiniment petits à notre échelle, mais contenant encore un nombre suffisant de molécules pour que les grandeurs attachées à ces éléments de volume soient des fonctions continues des coordonnées.

Les méthodes théoriques de détermination des champs de vitesses et de contraintes impliquent la résolution d’équations aux dérivées partielles non linéaires, tâche que l’on confie maintenant aux ordinateurs. Les études expérimentales peuvent s’effectuer soit directement, comme dans les autres sciences, soit sur des modèles réduits, placés dans des souffleries aérodynamiques ou hydrauliques, ou encore dans des bassins de carènes. Les réflexions sur la façon de passer des résultats obtenus sur des modèles réduits aux valeurs correspondant à la vraie grandeur ont donné naissance à l’analyse dimensionnelle: les phénomènes dépendent de nombres sans dimensions, dont les valeurs doivent être les mêmes pour le modèle réduit et le cas réel.

Les lois de la mécanique des fluides se sont dégagées peu à peu à partir d’une technique plusieurs fois centenaire, l’hydraulique; mais c’est la naissance de l’aviation qui a fait faire d’immenses progrès en ce domaine. La mécanique des fluides possède des applications techniques, mais elle fournit également des schémas d’explication pour l’océanographie physique et la mécanique de l’atmosphère ainsi que pour certaines branches de la physique du globe et de l’astrophysique. La mécanique des fluides, enfin, a été étendue à l’étude d’écoulements plus compliqués, qui concernent des fluides d’une nature particulière (fluides conducteurs dans un champ magnétique, fluides non newtoniens), ou encore des fluides soumis à des conditions spéciales (gaz raréfiés, filtration à travers un milieu poreux).

1. Cinématique des fluides

Champ des vitesses

Imaginons à l’intérieur d’un fluide une surface fermée entourant un point M, à l’intérieur de laquelle se trouvent, à un instant donné t , un certain nombre de molécules dont le centre d’inertie se déplace avec une certaine vitesse. Lorsque les dimensions de la surface tendent vers zéro, cette vitesse tend vers un vecteur appelé vitesse ふ du fluide au point M et à l’instant t . On définit ainsi un champ de vecteurs, appelé champ de vitesses du fluide . Les dimensions de la surface fermée ne doivent pas être trop faibles au cours de ce passage à la limite; il faut que les molécules qu’elles renferment restent en nombre suffisant pour que la vitesse soit une fonction continue.

Une particule fluide est une surface fermée infiniment petite se déplaçant avec le fluide, c’est-à-dire telle que chacun de ses points soit animé de la même vitesse locale que le fluide. Le mouvement de cette particule peut se décomposer en un mouvement de translation dont la vitesse est celle du centre d’inertie du fluide contenu dans la surface fermée et en un mouvement de rotation dont le vecteur vitesse de rotation est:

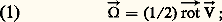rotふ est un vecteur appelé rotationnel de la vitesse qui a pour composantes dans un référentiel cartésien fixe:

respectivement le long de l’axe des x , de l’axe des y et de l’axe des z .

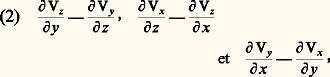Les écoulements de fluides pour lesquels le rotationnel du champ des vitesses est partout nul sont dits écoulements irrotationnels. C’est le cas, par exemple, des écoulements de fluides non visqueux autour d’obstacles lorsqu’il n’y a pas de surfaces de discontinuité de pression (ondes de chocs).

En dehors du mouvement de translation et de rotation, la particule fluide peut se déformer de telle façon que, si cette particule était à l’origine une sphère, elle se transformerait par affinité en ellipsoïde.

On appelle trajectoires du fluide les trajectoires des centres d’inertie des particules fluides. Si l’écoulement du fluide est permanent, c’est-à-dire si le champ des vitesses ne dépend pas du temps, les trajectoires sont des lignes invariables appelées lignes de courant tangentes à la vitesse locale. On a alors le système:

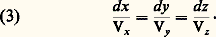Les lignes de courant s’appuyant sur une courbe fermée forment un tube de courant à travers lequel s’écoule un débit massique constant.

Loi de conservation de la masse

Considérons un petit élément de volume parallélépipédique fixe de dimensions dx , dy et dz . Le bilan de la masse du fluide entrant et sortant par les faces de l’élément de volume fournit une équation dite de continuité ou de conservation de la masse:

福(x, y, z, t ) est la masse volumique du fluide au point M, c’est-à-dire le rapport de la masse du fluide, contenu dans l’élément de volume à l’instant t , et du volume dx dy dz .

2. Statique des fluides

Théorème d’Archimède

Soit une surface finie plongée dans un fluide au repos. Le fluide placé d’un côté de cette surface exerce sur le fluide placé de l’autre côté des efforts appelés efforts de pression. Lorsque la surface est infiniment petite et d’aire d 靖, la résultante de ces efforts de pression est une force infiniment petite, perpendiculaire à la surface, qui s’écrit:

où ょ est le vecteur unitaire normal à la surface. Le scalaire p est indépendant de l’orientation de l’élément de surface autour du point considéré, et est appelé pression statique du fluide ou, tout simplement, pression. Dans un champ de pesanteur, la pression du fluide n’est pas uniforme. En effet, l’équilibre des forces de pression et de pesanteur agissant sur un élément de volume s’exprime sous la forme:

g étant l’accélération de la pesanteur et z l’altitude comptée positivement vers le haut.

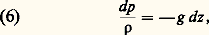Lorsque le fluide peut être considéré comme peu compressible, ce qui est le cas des liquides, la relation (6) est équivalente à:

où p est une constante appelée pression motrice. La pression est donc uniforme sur des plans horizontaux et croît linéairement avec la profondeur.

En conséquence, les forces de pression sur un corps plongé dans un fluide ont pour résultante une force dirigée vers le haut égale et opposée au poids du fluide déplacé, et dont le support passe par le centre d’inertie de ce fluide. Cela constitue le théorème d’Archimède.

Loi de Laplace

Deux fluides non miscibles sont séparés par une interface le long de laquelle existe une tension superficielle 靖. C’est le rapport de la force qui s’exerce de part et d’autre d’un élément de courbe placé sur l’interface à la longueur de cet élément.

Lorsqu’il y a passage à travers une interface, il existe une discontinuité de la pression qui obéit à la loi de Laplace: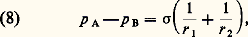

où r ¹ et r ² sont les rayons de courbure principaux de l’interface, le fluide A étant du côté de la concavité.

Loi de Jurin

Lorsqu’un tube cylindrique vertical de rayon r est plongé partiellement dans un liquide, le liquide s’élève en général à une hauteur h , donnée par la loi de Jurin:

est l’angle, appelé angle de contact, que fait le ménisque avec la paroi intérieure du tube. Remarquons que, dans le cas du mercure contenu dans un tube en verre, il y a dépression du liquide (h 麗 O): le ménisque est au-dessous de la surface libre.

3. Dynamique des fluides

Tenseur des contraintes

Lorsqu’un fluide est en mouvement, la résultante des efforts exercés par le fluide placé d’un côté d’un élément de surface sur le fluide placé de l’autre côté est une force élémentaire d F porportionnelle à l’aire d 靖 de l’élément de surface:

ゝ est un vecteur, appelé contrainte du fluide, qui dépend de l’orientation de l’élément de surface. On montre que ce vecteur prend la forme (11) du tableau, où 見, 廓 et 塚 sont les cosinus directeurs de la normale à l’élément de surface. Le tableau constitué par les neuf composantes 精^xx, 精^xy, 精^xz,... est appelé le tenseur des contraintes du fluide. Il est symétrique par rapport à la diagonale et ses composantes sont des fonctions des coordonnées et du temps.

Loi de comportement

Le champ tensoriel des contraintes est lié au champ vectoriel des vitesses par une expression appelée loi de comportement du fluide. Pour un gaz ou un liquide ordinaire (à l’exclusion des suspensions et des solutions de macromolécules), il existe des relations linéaires entre les composantes du tenseur des contraintes et les dérivées partielles d’espace des composantes de la vitesse, qui sont également au nombre de neuf. On dit alors que le fluide est newtonien: dans l’équation (12), les indices i et k peuvent être remplacés par x , par y ou par z , les variables indépendantes indicées étant x ¹ = x , x ² = y et x ³ = z ; le symbole de Kronecker 嗀^ik est égal à 1 si les indices i et k sont identiques, et à 0 si ces indices sont différents; 猪 est le coefficient de viscosité dynamique. Le rapport 益 = 猪/ 福 de la viscosité à la masse volumique est appelé viscosité cinématique.

Équations de Navier-Stokes

La différence entre les quantités de mouvement entrant et sortant par les faces d’un élément de volume parallélépipédique fixe est égale à la résultante des forces appliquées à cet élément, c’est-à-dire à la résultante des forces dues aux contraintes sur les faces et des forces volumiques.

Cela s’exprime par l’équation (13), où l’indice i est remplacé successivement par x, y et z . D ( 福Vⁱ )/Dt est une composante de la dérivée particulaire du vecteur 福 ふ, quantité de mouvement volumique du fluide. Cette dérivée doit son nom au fait qu’elle est la dérivée par rapport au temps du vecteur 福 ふ dans un référentiel qui se déplace avec la particule fluide (14). Fⁱ est une composante du champ vectoriel des forces volumiques, c’est-à-dire, par exemple, composante du champ de gravitation, du champ des forces centrifuges et des forces de Coriolis (pour les fluides en rotation par rapport à un référentiel fixe), du champ des forces de Lorentz (pour les fluides conducteurs dans un champ magnétique) ou de leurs combinaisons.

Si l’on introduit la loi de comportement (12) dans l’équation (13) de conservation de la quantité de mouvement, on obtient un système de trois équations non linéaires aux dérivées partielles du second ordre appelées équations de Navier-Stockes (15), où les indices i , k, l sont obtenus par permutation circulaire des nombres 1, 2, 3.

Pour résoudre les équations et obtenir le champ des vitesses, par exemple autour d’un obstacle, il faut tenir compte des conditions aux limites à satisfaire:

– sur les obstacles solides, il doit y avoir égalité des vitesses locales du fluide et du solide (condition de non-glissement);

– sur les interfaces avec un autre fluide non miscible, il doit y avoir non seulement égalité des vitesses des deux fluides, mais encore égalité des contraintes tangentielles. En outre, les contraintes normales doivent satisfaire à la loi de Laplace (8).

La description complète d’un écoulement nécessite la connaissance des champs de vitesse, des champs de pression et de la masse volumique en chaque point. Il faut ainsi déterminer cinq fonctions des coordonnées spatiales et du temps à l’aide des cinq équations constituées par les trois équations de Navier-Stokes (15), par l’équation de continuité (4) et par l’équation d’état qui lie la pression, la masse volumique et la température. Si la masse volumique ne peut être considérée comme uniforme, il faut, pour déterminer le champ des températures, faire intervenir l’équation de conservation de l’énergie (16), où 阮 est une fonction de dissipation (17) qui correspond à la production de chaleur par le frottement interne, h l’enthalpie massique et la conductivité thermique ^{[cf. THERMODYNAMIQUE]}.

Les équations de Navier-Stokes (15) et l’équation de conservation de l’énergie (16) sont souvent transformées pour faire apparaître des variables réduites qui sont d’un grand intérêt pratique. En effet, on peut déterminer les champs de pression et de vitesse autour d’obstacles tels que des avions ou des navires en opérant sur des modèles réduits placés dans des souffleries ou des bassins de carène.

Pour cela, il faut que certains nombres sans dimensions aient les mêmes valeurs pour le modèle réduit et pour le cas réel. On montre, grâce au théorème de Vaschy-Buckingham (cf. analyse et similitude DIMENSIONNELLES), que le nombre des nombres sans dimensions est égal à la différence entre le nombre de grandeurs physiques intervenant dans le phénomène physique et le nombre de dimensions qui composent les grandeurs. Pour la mécanique des fluides isovolumes, il y a trois dimensions: la masse, la longueur et le temps. Si la masse volumique ne peut plus être supposée constante, il y a une dimension de plus, la température.

Équations d’Euler

Si les effets de la viscosité sont négligeables, les équations de Navier-Stokes (15) se simplifient. Elles forment alors un système d’équations aux dérivées partielles non linéaires du premier ordre (18), appelées équations d’Euler, qui régissent donc des fluides hypothétiques que l’on désigne sous le nom de fluides parfaits.

Sur une paroi solide, la condition de non-glissement n’est plus imposée, mais il doit y avoir égalité des vitesses normales du fluide et du solide.

Si les effets de la conductivité thermique sont également négligeables, c’est-à-dire si le nombre de Prandtl 戮r = 猪c ^p /, où c ^p est la chaleur massique à pression constante, n’est pas trop faible, l’équation de conservation de l’énergie (16) se simplifie également et l’on aura l’équation (19) le long d’une ligne de courant, h ^t étant une intégrale première appelée enthalpie totale du fluide.

Loi globale d’Euler

Soit une surface fermée fixe S, dite surface de contrôle entourant un volume V. Le système des densités de flux des quantités de mouvement normales à cette surface est équivalent au système des forces de contact agissant sur cette surface et des forces volumiques. On peut écrire l’égalité (20) entre les résultantes des deux systèmes; cette relation permet de calculer, dans de nombreux cas, l’effort total exercé sur un obstacle.

4. Écoulements de fluides parfaits

Écoulements incompressibles

Lorsque les valeurs maximales des vitesses d’écoulement et des différences de température entre les obstacles et le fluide sont faibles, on peut considérer que la masse volumique reste pratiquement constante. Les écoulements sont alors appelés incompressibles. L’équation de conservation de la quantité de mouvement (18), sous la forme donnée par Euler, devient alors: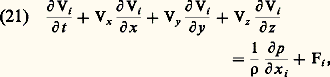

ou encore:

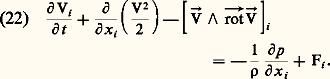Cette dernière forme se simplifie pour les écoulements irrotationnels.

Écoulements unidimensionnels

Un écoulement qui se produit dans une conduite dont la section varie lentement peut être étudié approximativement en supposant que la vitesse ふ est perpendiculaire à la section droite et uniforme dans cette section. La vitesse ne dépend donc que d’une seule dimension, l’abscisse curviligne de l’axe de la conduite, d’où le nom d’écoulement unidimensionnel donné à ce type d’écoulement.

En intégrant les équations (22), on obtient, pour un écoulement permanent, dans le cas où les forces volumiques sont les forces de pesanteur, la relation de Bernoulli:

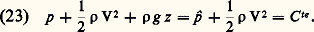Le binôme p + (1/2) 福 V², somme de la pression statique p et de la pression dynamique ( 福 V²)/2, est appelé pression totale de l’écoulement. Cette pression totale est constante, si l’on ne tient pas compte des effets de la petanteur.

En outre, le débit massique à travers la conduite est constant:

A étant l’aire de la section droite.

La relation de Bernoulli et la relation (24) permettent, par exemple, de montrer que, dans un tube de Venturi, qui est une tuyère convergente-divergente, autrement dit une tuyère dont la section passe par un minimum, la différence de pression entre le col et l’entrée de la tuyère est proportionnelle au carré du débit qui la traverse.

La relation (23) s’applique également le long d’une ligne de courant générale d’un écoulement irrotationnel.

Écoulements bidimensionnels

Un écoulement bidimensionnel est un écoulement dont les vitesses sont toutes parallèles à un plan et dont les composantes des vitesses ne dépendent que des coordonnées de ce plan. Dans un écoulement bidimensionnel, irrotationnel et permanent, la vitesse dépend d’un potentiel 淋 (x, y ):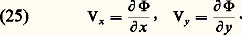

Ce potentiel est harmonique, c’est-à-dire qu’il obéit à l’équation de Laplace:

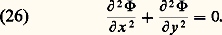D’après l’équation de conservation de la masse (4), on a:

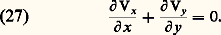On en tire les relations suivantes:

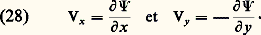切 (x, y ), appelée fonction de courant, est également une fonction harmonique:

Le long des lignes de courant, 切 est constant. D’après les relations (25) et (28), les lignes de courant sont orthogonales aux lignes équipotentielles qui sont les lignes le long desquelles 淋 reste constant.

On groupe le potentiel et la fonction de courant sous la forme d’un expression binôme, dite potentiel complexe: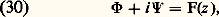

où i = 連 漣 1 et où F(z ) est une fonction analytique de la variable complexe z = x + iy , c’est-à-dire une fonction dont la dérivée ne dépend pas de la façon dont on fait varier la différentielle dz . Cette dérivée s’écrit:

et s’appelle vitesse complexe. Voici quelques exemples de potentiels complexes.

Pour un écoulement uniforme:

la constante étant un nombre complexe quelconque.

Pour un écoulement autour d’une source ou d’un puits placé en un point d’affixe z ⁰: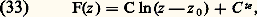

C étant un nombre réel.

On peut construire d’autres écoulements en superposant des écoulements de ce type ou encore en utilisant la représentation conforme qui permet de passer d’un écoulement bidimensionnel à un autre écoulement bidimensionnel par une transformation convenable des coordonnées.

Écoulements de fluides compressibles

Nombre de Mach

Pour un gaz parfait, l’équation d’état est de la forme:

où R = 8 314 J mole^{-1 0}C^-1 est la constante des gaz parfaits et M la masse moléculaire du gaz.

Les petites variations de la pression se propagent par rapport au fluide avec une célérité c , appelée célérité du son, qui est donnée par la formule: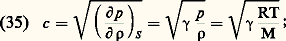

(face=F0019 煉p / 煉 福)^s est la dérivée partielle de la pression par rapport à la masse volumique pour une entropie S constante. 塚 = c ^p /c ^v est le rapport des chaleurs massiques à pression et à volume constants du gaz, pour une valeur de 塚 = (3 + 2 n )/(1 + 2 n ), n étant le nombre d’atomes de la molécule gazeuse.

Lorsque les vitesses ふ d’un écoulement ne peuvent plus être considérées comme négligeables par rapport à la célérité du son, il faut abandonner l’hypothèse de l’invariabilité de la masse volumique. Cette masse volumique est alors une fonction du nombre de Mach local face=F9796 M, rapport de la vitesse locale V à la célérité locale du son c :

Si le nombre de Mach à l’infini amont face=F9796 M 秊 est inférieur à l’unité, on dit que l’écoulement est subsonique . Si face=F9796 M 秊 est supérieur à l’unité, l’écoulement est dit supersonique . Lorsque face=F9796 M 秊 est voisin de l’unité, on parle d’écoulement transsonique, l’écoulement présentant alors des parties subsoniques et des parties supersoniques. Dans le cas d’un écoulement supersonique, les petites perturbations de pression en un point se propagent le long d’un cône, appelé cône de Mach. Ce cône a pour axe la direction de la vitesse et pour demi-angle l’angle de Mach: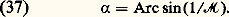

Les lignes qui sont constamment tangentes aux génératrices du cône de Mach local sont les caractéristiques ou les lignes de Mach de l’écoulement.

Le nombre de Mach peut avoir une valeur aussi grande que l’on veut. Lorsque face=F9796 M 秊 礪 5, on a coutume de parler d’écoulements hypersoniques. La valeur 5 n’a rien de critique, mais c’est environ à partir de cette valeur que certains effets physiques prennent de l’importance, par exemple, la dissociation de l’air.

Écoulements isentropiques unidimensionnels

Dans une conduite, l’équation de conservation de la masse s’écrit:

et se met, sous forme différentielle, de la façon suivante: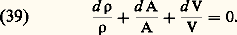

L’équation de conservation de la quantité de mouvement devient, lorsqu’on néglige la pesanteur:

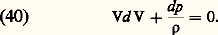Dans le cas d’un écoulement adiabatique d’un fluide idéal, en l’absence d’ondes de choc, l’entropie reste constante dans la conduite et la pression est reliée à la masse volumique par l’expression de la compression isentropique:

ou sous forme différentielle: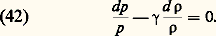

En combinant ces relations différentielles, on aboutit à l’équation:

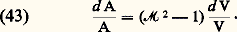Ainsi, dans une zone subsonique (face=F9796 M 麗 1), la vitesse V et l’aire A varient en sens inverse, tandis que, dans une zone supersonique (face=F9796 M 礪 1), la vitesse et l’aire varient dans le même sens. La vitesse ne peut être égale à la célérité locale du son qu’en une section d’aire minimale.

Dans une tuyère convergente-divergente, comme celle d’une soufflerie supersonique ou celle d’une fusée, la détente commence dans le convergent jusqu’à un nombre de Mach unité au col, puis continue dans le divergent, tandis que, pour les écoulements subsoniques, la détente dans le convergent est suivie d’une recompression.

L’équation de conservation de l’énergie s’exprime en écrivant que la somme de l’enthalpie h et de l’énergie cinétique par unité de masse est constante:

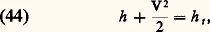où h ^t est l’enthalpie totale, enthalpie de l’écoulement pour une vitesse nulle.

Si la chaleur massique à pression constante du gaz ne varie pas avec la température, la relation (44) devient:

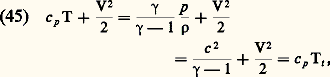où T^t est la température totale, température du fluide pour une vitesse nulle.

Entre deux sections d’indices 1 et 2, la relation (45), compte tenu de (41), prend la forme dite équation de Saint-Venant:

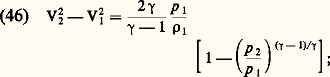Le long d’une ligne de courant, un certain nombre de relations valables pour un écoulement isentropique peuvent être déterminées. La pression est une fonction du nombre de Mach:

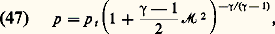p ^t est la pression totale, pression que l’on a dans l’écoulement pour une vitesse nulle, c’est-à-dire pour face=F9796 M = 0.

La température absolue est aussi une fonction du nombre de Mach:

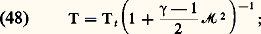la température baisse donc au cours d’une détente isentropique.

Dans une soufflerie, la pression et la température totales sont pratiquement égales à la pression et à la température dans le réservoir qui contient le gaz destiné à se détendre dans la tuyère, car les vitesses y sont très faibles.

Enfin, d’après la loi des gaz parfaits (34), la masse volumique s’écrit:

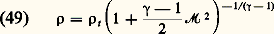Ondes de choc droites

Une onde de choc est une surface à travers laquelle se produit une variation brusque de la pression. Dans un tube cylindrique, si l’on brise un diaphragme séparant deux régions à pressions différentes, une onde de choc se propage dans le gaz où règne la plus faible pression. Cette onde de choc est normale à l’axe du tube et aux vitesses de l’écoulement; on l’appelle onde de choc droite.

Dans un système de coordonnées qui se déplace à la même vitesse que l’onde de choc, on a de part et d’autre de l’onde de choc:

l’indice 1 correspondant à l’amont et l’indice 2 à l’aval. L’équation de Saint-Venant est valable à l’amont comme à l’aval: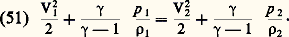

Si l’on prend comme surface de contrôle un cylindre fini dont les génératrices sont perpendiculaires à l’onde de choc et qui est traversé par celle-ci, la loi globale d’Euler (20) donne l’équation:

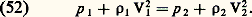À l’aide des trois relations de RankineHugoniot (50), (51) et (52) on obtient tout d’abord la formule de Prandtl:

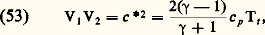où c est la célérité du son que l’on obtiendrait en amenant isentropiquement l’écoulement à une vitesse correspondant à un nombre de Mach unité.

Le rapport des pressions amont et aval s’écrit:

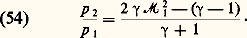En outre, entre les nombres de Mach amont et aval existe la relation suivante:

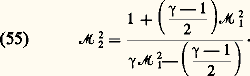On n’observe jamais que des ondes de choc de compression, c’est-à-dire telles que p ² 礪 p ¹, le nombre de Mach amont face=F9796 M² étant toujours supersonique et le nombre de Mach aval face=F9796 M¹ toujours subsonique. En effet, la compression à travers une onde de choc augmente l’entropie du gaz, ce qui est conforme au deuxième principe de la thermodynamique.

Ondes de choc obliques

Devant un obstacle se déplaçant à vitesse supersonique, il se forme une onde de choc, «détachée» si l’avant de l’obstacle est arrondi, comme dans le cas d’une capsule rentrant dans l’atmosphère, ou «attachée» si l’avant est anguleux ou pointu.

Si l’obstacle a la forme d’un dièdre dont l’arête est perpendiculaire à la vitesse à l’infini, l’onde de choc est plane et fait un certain angle avec la vitesse de l’écoulement amont. C’est une onde de choc oblique, derrière laquelle l’écoulement est uniforme et parallèle à la surface du dièdre.

Les relations (50), (51) et (52) restent valables si l’on remplace V¹ et V² par les vitesses normales à l’onde de choc. Il faut y ajouter la condition d’égalité des vitesses tangentielles.

Une ligne de courant à l’amont d’une onde de choc non plane est rectiligne jusqu’à son intersection avec l’onde de choc. La relation entre les pressions de part et d’autre de cette intersection est la même que celle qui existe à travers l’onde de choc oblique tangente en ce point à l’onde de choc non plane.

Devant un cône placé dans un écoulement supersonique et dont l’axe est parallèle à la vitesse à l’infini, il se produit une onde de choc conique ayant pour sommet et pour axe le sommet et l’axe du cône. Derrière cette onde de choc conique, la pression augmente le long des lignes de courant à mesure que l’on se rapproche de la surface de l’obstacle; on a alors un écoulement conique, c’est-à-dire tel que la pression et la vitesse sont uniformes sur des cônes situés entre l’obstacle et l’onde de choc et ayant le même sommet et le même axe que le cône obstacle.

Écoulements à surface libre

Il semble logique de distinguer, dans le comportement des fluides présentant une surface libre (essentiellement interface eau-air), les cas où il y a transport de matière de ceux où il n’y en a pas. Cependant, ces deux domaines font appel aux mêmes équations de l’hydrodynamique, essentiellement les principes de conservation de la masse et de la quantité de mouvement. Si l’hypothèse du fluide parfait, associée à l’incompressibilité, rend les problèmes plus abordables, les conditions aux limites sont bien souvent non linéaires, et il est nécessaire d’aller plus loin dans la schématisation pour obtenir des solutions explicites.

Régime fluvial, régime torrentiel

Selon qu’un écoulement en canal, ou un cours d’eau, a une vitesse inférieure, égale ou supérieure à une vitesse critique V^c , il est qualifié de fluvial, critique ou torrentiel. C’est le nombre de Froude, 杻, exprimant le rapport entre les forces d’inertie et les forces de gravité, qui détermine la limite entre ces différents domaines. En régime torrentiel, par exemple, une perturbation sur la surface libre ne pourra être ressentie en amont et sa zone d’influence sera limitée vers l’aval par deux frontières obliques, inclinées d’un angle 見 par rapport à la direction de la vitesse moyenne tel que:

En eau peu profonde, on constate une analogie frappante entre un tel comportement et celui d’un écoulement plan de gaz compressible à grande vitesse (cf. chap. 4 Écoulements de fluides compressibles ). Le nombre de Mach face=F9796 M et le nombre de Froude 杻 jouent des rôles équivalents. Le passage de l’état fluvial à l’état torrentiel s’effectue de façon quasi isentropique. Le passage inverse, par contre, s’accompagne d’une dissipation d’énergie localisée dans un ressaut assimilable à un choc de recompression.

Ondes de surface

L’étude des ondes de surface et de leur propagation, partie intégrante de la mécanique des fluides, est d’une grande importance si l’on songe aux différents domaines dans lesquels celle-ci est susceptible de trouver une application. Citons comme exemple le phénomène des marées, avec la houle et ses effets sur les ouvrages maritimes et les navires, mais aussi son rôle dans la résistance à l’avancement des bateaux.

Plusieurs théories sont utilisées pour décrire le comportement de la surface de la mer. Celles d’Airy, de Gerstner et de Stokes sont les plus courantes. Elles supposent toutes l’absence de viscosité, une profondeur d’eau constante et des gradients de température et de masse volumique négligeables. Enfin, la force de pesanteur est la seule force extérieure à laquelle le fluide est soumis. Les équations de base d’un tel écoulement, plan, incompressible, et la plupart du temps considéré comme irrotationnel, sont l’équation de Laplace (déduite de l’équation de continuité), à savoir:

淋 étant le potentiel des vitesses, et l’équation de Bernoulli: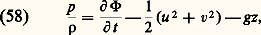

où p et 福 sont respectivement la pression locale et la masse volumique de l’eau en un point de cote verticale z , u et v les composantes dans un plan vertical de la vitesse d’une particule d’eau située à la cote z .

Les conditions aux limites associées sont:

– au fond, la condition d’imperméabilité, soit v = 0;

– à la surface libre, une double condition, exprimant le fait que la pression y est partout égale à la pression atmosphérique et aussi qu’une particule liquide, y étant initialement située, y reste au cours du temps.

La théorie d’Airy est la plus simple. Pente et élévation de la surface libre sont supposées faibles. Les termes quadratiques des composantes de la vitesse sont négligés. Malgré ces approximations, les relevés expérimentaux corroborent de façon satisfaisante dans la plupart des cas les valeurs théoriques. Pour des profondeurs d’eau supérieures à une demi-longueur d’onde (cas relativement fréquent), les expressions donnant les différents paramètres de l’onde se simplifient notablement. Ainsi, la célérité, ou vitesse de phase, d’une onde progressive est proportionnelle à sa période: C = g T/2 神. On démontre facilement que les trajectoires des particules d’eau sont des ellipses dans le cas général (des cercles en profondeur infinie). La vitesse de parcours de ces orbites ne doit être confondue ni avec la célérité précédente ni avec la vitesse de transport de l’énergie de l’onde, ou vitesse de groupe. En profondeur infinie, cette dernière est égale à la moitié de la célérité.

Les ondes que nous venons d’évoquer sont des ondes de pesanteur auxquelles il faut associer des rayons de courbure instantanés relativement grands. À l’opposé, les rides observables à la surface de l’eau et dont les longueurs d’onde caractéristiques sont de l’ordre du centimètre sont appelées ondes capillaires. La tension superficielle est à ce moment la force prépondérante.

Il existe une limite supérieure de la hauteur de l’onde à partir de laquelle on peut observer le déferlement. La vitesse d’une particule d’eau située à la crête de la vague est alors égale ou supérieure à la célérité de l’onde. Ce phénomène se produit lorsque les ondes rencontrent une plage inclinée, ou lorsque, au large, donc en profondeur pratiquement infinie, il y a interférence constructive entre ondes de différentes périodes. Pour fixer les idées, sans déferlement, le rapport de la hauteur crête/creux à la longueur d’onde ne peut excéder un septième.

Ondes stationnaires. Clapotis

Une houle incidente frappant une digue verticale se réfléchit totalement. Tout est comme si, au voisinage de celle-ci, deux ondes de même longueur et de même hauteur se propageaient en sens inverse. La hauteur de l’onde résultante se trouve donc être pratiquement le double de celle de l’onde incidente. La surface libre comporte des ventres distants de KL/2, K étant un nombre entier et L la longueur d’onde. Les nœuds d’amplitude se situent à mi-distance des ventres. L’équation de la surface libre s’écrit:

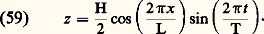Au sein du fluide, les trajectoires des particules sont de petits tronçons d’arc dont les enveloppes déterminent les lignes de courant. Pression et vitesse peuvent être calculées partout dans le champ fluide, et en particulier sur la digue (efforts instationnaires permettant le dimensionnement convenable de l’ouvrage) et sur le fond (maximum des vitesses indiquant les zones d’érosion privilégiées).

Phénomènes dispersifs

Les lignes précédentes ne concernent que des ondes sinusoïdales simples où les oscillations qu’exécutent les diverses particules d’un même plan horizontal ne diffèrent les unes des autres que par leur phase. À la houle, ou d’une façon plus générale aux mouvements naturels d’une surface liquide, il faut associer la notion de distribution spectrale de longueurs d’onde. La célérité étant fonction de L, le phénomène de propagation va présenter une dispersion, de façon analogue à la propagation de la lumière. On peut démontrer que, en eau profonde, la vitesse d’une onde de gravité augmente avec sa longueur:

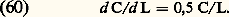Lorsqu’on est confronté à une multitude d’ondes de longueurs différentes se propageant dans la même direction et interférant de façon destructive ou constructive, on conçoit la difficulté d’une telle étude mathématique.

Ondes de marée

Les marées sont des oscillations forcées causées par l’attraction conjuguée de la Lune et du Soleil, et de ce fait possèdent les mêmes périodes que le mouvement de ces astres par rapport à la Terre. Ces périodes se comptent en heures et, par conséquent, les «vagues» associées ont des longueurs d’onde de plusieurs centaines de kilomètres. Le rapport profondeur/longueur d’onde se révèle donc être très petit et il est naturel de songer à entreprendre l’étude du phénomène en utilisant la formulation simplifiée des ondes en eau peu profonde. Hélas, une difficulté majeure subsiste, celle qui consiste à exprimer de façon réaliste les conditions aux limites: effets dissipatifs et profondeurs pratiquement nulles à proximité des côtes. Les annuaires des marées sont encore établis à partir de relevés statistiques. Les modèles mathématiques approchés constituent cependant une aide qualitative.

5. Écoulements de fluides visqueux

Écoulements dans les conduites

Écoulement laminaire

L’écoulement d’un fluide visqueux dans une conduite rectiligne s’effectue de telle façon que les lignes de courant glissent les unes sur les autres tout en restant parallèles; l’écoulement est alors appelé laminaire. La non-uniformité des vitesses introduit dans le fluide des contraintes d’origine visqueuse dont l’expression est donnée par la loi de comportement (12).

Dans une conduite de section circulaire et de diamètre d , la condition de nonglissement à la paroi conduit à un profil de vitesses parabolique. La loi globale d’Euler (20) montre que la différence de la pression motrice p = p + 福gz entre deux sections de la conduite d’indices 1 et 2, c’est-à-dire la perte de charge, est proportionnelle à la vitesse moyenne ou vitesse de débit volumique V^q , quotient du débit par l’aire de la section. On a ainsi la formule de Poiseuille pour une conduite de longueur L:

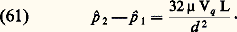Cette formule peut être transposée sous une forme adimensionnelle, en introduisant le nombre de Reynolds de la conduite:

rapporté à la vitesse moyenne V^q et au diamètre de la conduite d .

On appelle coefficient de perte de charge le nombre sans dimensions: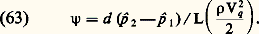

Ce nombre est inversement proportionnel au nombre de Reynolds. En effet, la formule de Poiseuille donne:

Écoulement turbulent

Lorsque le nombre de Reynolds atteint la valeur de 2 200 environ, l’écoulement devient turbulent, c’est-à-dire que les vitesses dans la conduite varient de façon aléatoire. Les profils des vitesses moyennes par rapport au temps ne sont plus paraboliques, mais elles ont une forme plus aplatie. Tout se passe comme si les vitesses moyennes obéissaient aux équations de Navier-Stokes, compte tenu de contraintes supplémentaires appelées contraintes de Reynolds: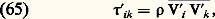

les V ⁱ et les V ^k étant les fluctuations de vitesse (différences entre les vitesses instantanées et les vitesses moyennes) et la barre supérieure correspondant à une moyenne dans le temps.

Ces contraintes sont responsables de l’augmentation de perte de charge dans une conduite circulaire lorsque l’écoulement y est turbulent. En effet, la formule (64) doit être remplacée par la formule de Prandtl, relation implicite entre le coefficient de perte de charge et le nombre de Reynolds:

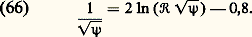Dans les écoulements compressibles, on constate également des fluctuations de masse volumique et de température qui sont reliées aux fluctuations de vitesse.

Écoulements à faibles nombres de Reynolds

Dans le cas des écoulements autour d’un obstacle donné, il n’existe aucune méthode générale d’intégration des équations de Navier-Stokes, sauf si le nombre de Reynolds est très grand ou très petit. Ce dernier cas correspond à des obstacles de très petites dimensions ou se déplaçant à très faible vitesse; on le rencontre physiquement dans le mouvement des micro-organismes ou encore dans celui des suspensions (brouillards, aérosols, sédimentation, etc.).

De tels mouvements sont caractérisés par le fait que les forces d’inertie sont négligeables devant les forces de viscosité, et les équations de Navier-Stokes se simplifient en première approximation sous la forme:

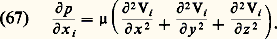On a pu intégrer facilement ces équations linéaires pour des obstacles tridimensionnels de forme simple, tels qu’une sphère de diamètre d , pour laquelle la force de traînée a été obtenue par Stokes sous la forme:

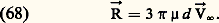En revanche, on a pu montrer qu’il n’existe pas de solution dans le cas de l’écoulement bidimensionnel autour d’un cyclindre (paradoxe de Stokes) et que la même difficulté se retrouve en écoulement tridimensionnel si on recherche la seconde approximation de la solution (paradoxe de Whitehead). Ces deux paradoxes n’ont été levés qu’en 1954 par la mise au point et l’utilisation d’une nouvelle méthode de perturbation dite «méthode des développements asymptotiques raccordés».

On a pu ainsi montrer que l’équation (67) n’était pas valable au voisinage de l’infini où elle devait être remplacée par celle dite d’«Oseen»; on a alors, par addition de deux développements asymptotiques, déterminé l’écoulement autour d’un cylindre et trouvé les approximations suivantes pour la sphère. Dans ce dernier cas, on a montré notamment que la traînée était donnée par la formule plus précise:

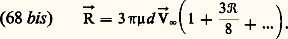Couche limite

Dans le cas d’écoulements fluides autour d’obstacles, pour lesquels la distribution de pression mesurée est à peu près en accord avec la théorie de fluide parfait, l’influence de la viscosité aux grands nombres de Reynolds est limitée à une très fine couche située au voisinage immédiat du corps, par exemple un profil d’aile. L’étude expérimentale montre que la vitesse V du fluide augmente de zéro à la paroi (adhérence imposée par les forces d’attraction intermoléculaires) jusqu’à une valeur correspondant à celle de l’écoulement externe sans frottement. Cette mince zone est appelée couche limite. Son concept est dû à Ludwig Prandtl.

Les contraintes tangentielles sont là considérables, même lorsque la viscosité 猪 est faible, car les gradients de vitesse sont importants. Le cisaillement 精^p à la paroi (y = 0) s’écrit:

Son intégration sur toute la surface d’un objet, mouillée par le fluide, permet de déterminer la traînée de ce dernier et de lever ainsi le paradoxe de d’Alembert, résultant de l’hypothèse de fluide parfait. De plus, si ces forces de frottement ne sont pas directement responsables de la portance, ce sont elles qui, au départ, engendrent une circulation autour du corps.

Pour la plupart des cas réels, la couche limite n’est pas de nature homogène au cours de son évolution et, à l’image du comportement d’un fluide dans une conduite, une transition va s’effectuer d’un régime laminaire vers un régime turbulent. Cela se produit quand le nombre de Reynolds 倫^x , fondé sur la valeur de la vitesse de l’écoulement extérieur V^e à une abscisse x donnée, se trouve compris entre 3 憐 10⁵ et 5 憐 10⁵.

Il est classique, dans les calculs, d’introduire des coefficients, ou épaisseurs, permettant de caractériser la couche limite. Ce sont le coefficient de frottement pariétal et les différentes hauteurs 嗀, 嗀¹, 嗀², successivement épaisseur, épaisseur de déplacement, épaisseur de quantité de mouvement.

La couche limite n’adhère pas dans tous les cas à la paroi pendant tout le temps de son développement et, à un moment, peut survenir son décollement (cf. figure). Ce phénomène est toujours associé à la formation de gros tourbillons, initiateurs du sillage d’un obstacle par exemple.

Couche limite laminaire

Dans le cadre des équations de Navier (cf. chap. 3), donc pour des écoulements laminaires de fluides newtoniens, le schéma de couche limite est accessible, sous certains de ses aspects, à la théorie pure. C’est le cas de la plaque plane, sans incidence, en présence d’un gradient de vitesse nul, problème auquel correspond la solution de Blasius, impliquant une hypothèse d’affinité sur la loi de distribution des vitesses. Cette méthode conduit aux expressions suivantes des différentes épaisseurs caractéristiques de la couche limite: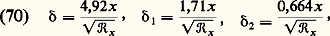

et, pour la contrainte tangentielle à la paroi:

En prenant en compte la conservation de la masse et en intégrant, de 0 à 嗀, l’équation de quantité de mouvement valable dans la couche limite, on obtient l’équation intégrale de Karman, qui exprime le frottement à la paroi 精^p en fonction des épaisseurs de quantité de mouvement et de déplacement: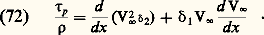

Cette équation est à la base de la plus grande partie des méthodes pratiques de calcul des couches limites, notamment celles qui utilisent des algorithmes numériques (différences finies ou éléments finis).

À la surface d’un obstacle, le gradient de la pression est rarement nul, et il peut s’opposer au développement régulier de la couche limite en provoquant son décollement. Cette éventualité peut être prévue par des méthodes plus ou moins raffinées. Celle de Pohlhausen est l’une des plus simples, mais suppose a priori que les profils de vitesses successifs obéissent à une loi polynomiale de degré quatre, de façon à satisfaire l’ensemble des conditions aux limites. Le calcul ne peut alors s’effectuer que jusqu’au point de décollement.

Couches limites turbulentes

Lorsque la turbulence est établie, les équations de Navier-Stokes demeurent valables pour décrire le mouvement instantané du fluide au sein de la couche limite, mais la résolution du problème devient impossible, du fait du caractère aléatoire des fluctuations de toutes les grandeurs physiques. C’est à Osborn Reynolds que revient l’idée d’introduire dans ces mêmes équations la décomposition en valeur moyenne et fluctuation de toutes les grandeurs physiques qui y interviennent. Ce sont les équations de Reynolds, dans lesquelles apparaissent six inconnues supplémentaires dans le cas le plus général au niveau du tenseur des contraintes, qui s’écrit habituellement:

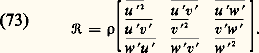u , v , w étant les composantes de la fluctuation de vitesse. La turbulence de couche limite n’est pas isotrope du fait de cette direction privilégiée qu’est le mouvement moyen et, pratiquement, seul le cisaillement turbulent suivant cette direction est important. Les termes diagonaux du tenseur de Reynolds sont l’équivalent de termes de pression supplémentaires, à associer aux pressions déduites de la solution potentielle extérieure. Ils définissent d’autre part un niveau ou degré de turbulence. On peut apprécier l’importance du cisaillement turbulent 漣 福u v lorsqu’on sait que, à une distance de la paroi de 4 p. 100 de la couche, il est déjà environ deux cents fois supérieur au cisaillement visqueux.

Le mécanisme de la turbulence de couche limite est étudié à partir de l’analyse spectrale des fluctuations autour de la valeur moyenne de la vitesse par exemple. On y constate entre autres que l’énergie décroît quand la fréquence augmente.

Les méthodes de calcul des couches limites turbulentes, même dans le cas relativement simple d’une plaque plane sans gradient de pression, restent des méthodes approchées. Elles demeurent fondées sur l’équation intégrale de quantité de mouvement qui, dans la mesure où le profil des vitesses moyennes est approximé par une relation empirique appropriée, fournit différentes relations entre les épaisseurs caractéristiques de la couche. Les lois empiriques de vitesse les plus utilisées sont les lois en puissance, ou les lois logarithmiques pour de plus grands nombres de Reynolds. En présence d’un gradient de pression et sur des parois non planes, il est nécessaire d’introduire un «facteur de forme» déduit de l’expérience. Parmi les méthodes de détermination les plus courantes, celle de Truckenbrodt possède l’originalité d’utiliser l’équation intégrale de l’énergie plutôt que celle relative aux quantités de mouvement.

Couche limite thermique

Il est naturel de penser que les domaines fluides dans lesquels se manifestent respectivement les phénomènes de frottement et de convection sont les mêmes. Effectivement, parallèlement à la couche limite dynamique, on peut définir une couche limite thermique, zone privilégiée du transport de chaleur entre une paroi chauffée ou refroidie et l’écoulement extérieur. Le nombre de Prandtl est le rapport entre la viscosité cinématique 益 et la diffusivité thermique a :

Suivant que ce rapport est inférieur, égal, ou supérieur à l’unité, la couche limite dynamique possède une épaisseur inférieure, égale, ou supérieure à la couche limite thermique. Outre le transfert de chaleur évoqué précédemment, et particulièrement dans le cas d’écoulements à grandes vitesses, on doit aussi considérer l’échauffement cinétique, dû au frottement.

L’introduction, dans le problème, de cette inconnue supplémentaire que constitue la température implique d’associer à l’équation de conservation de la masse et à celle des quantités de mouvement l’équation de l’énergie. Différentes épaisseurs caractéristiques, telles que l’épaisseur de déplacement thermique et l’épaisseur d’enthalpie, peuvent être définies, de même que le facteur thermique pariétal, ne dépendant pratiquement que de la nature du fluide (cas d’une paroi athermane uniquement). Une relation intégrale déduite de l’équation de la chaleur peut être associée à une méthode de Pohlhausen pour la prévision des bilans thermiques dans certains cas simples d’écoulements.

Couche limite en écoulement compressible

Ce sont les progrès dans le domaine aéronautique qui ont encouragé, ces dernières années, le développement des théories sur les couches limites en écoulement compressible. Quand les vitesses de vol atteignent plusieurs fois la vitesse du son, le travail de compression et la dissipation d’énergie produisent de grandes variations de température et le couplage entre le problème dynamique et le problème thermique est alors très étroit. De plus, les propriétés physiques des fluides telles que viscosité, chaleur spécifique, conductibilité ne peuvent plus être considérées comme des constantes. La masse volumique étant une nouvelle inconnue, on doit ajouter, aux trois équations de la couche limite thermique, l’équation d’état. Le problème devient donc fort complexe, mais peut cependant être approché, moyennant la linéarisation de certaines lois, telle celle de la viscosité en fonction de la température. Des transformations ont été découvertes (K. Stewartson), qui permettent de réduire les équations compressibles à la forme de celles de la couche limite incompressible.

6. Extensions de la mécanique des fluides

Les lois de la mécanique des fluides classique ont été étendues aux fluides conducteurs, tels que les plasmas et les métaux liquides s’écoulant dans un champ magnétique; cette extension constitue la magnétohydrodynamique (M.H.D.).

Pour les gaz raréfiés, dont l’étude est rendue nécessaire par les vols à haute altitude, la mécanique des fluides se transforme lorsque le nombre de Knudsen, rapport du libre parcours moyen des molécules à la plus grande dimension de l’obstacle, n’est plus négligeable devant l’unité. Lorsque le nombre de Knudsen augmente, par diminution de la pression par exemple, on peut tout d’abord conserver les équations de Navier-Stokes moyennant une condition de glissement sur les parois solides. Après avoir passé par un régime intermédiaire, on atteint finalement l’écoulement moléculaire libre dans lequel les molécules ne se rencontrent jamais.

Lorsqu’un fluide est contenu dans un milieu poreux, l’expérience montre que la moyenne spatiale des vitesses dans les pores est proportionnelle au gradient de la pression motrice du fluide. Cette loi, dite loi de Darcy, régit les écoulements dans les milieux poreux, tels que les terrains ou les couches rocheuses contenant de l’eau ou des hydrocarbures.

Encyclopédie Universelle. 2012.